Gibbs' Function

Students of thermodynamics are asked to keep three new concepts (free energy, enthalpy and entropy) in mind while trying to understand the importance of Gibbs' Function:

G = H - TS

After we open the valve in Figure 1, hydrogen flows from Tank B into Tank A. The metal hydrides inside the two tanks manifest free energy, enthalpy and entropy changes in ways that appeal to the intuition. Pressurized hydrogen gas, indicated on the pressure gauges of the HTT1, clearly has the ability to do work (ΔG) by moving a piston. As hydrogen gas is absorbed or desorbed, the heat of reaction (±ΔH) can be felt by touching the tanks. The evolution of a cloud of gas molecules (e.g., the background of this web page) from a crystalline solid represents an obvious increase in disorder (ΔS).

As metal hydride B (right side, Fig. 1) desorbs hydrogen gas, Tank B becomes cold to the touch (+ΔH flows in from the hand). Absorption by hydride A (left side, Fig. 1) makes Tank A hot to the touch (-ΔH flows out to the hand). This reinforces the notion that the terms in Gibbs' Function are signed quantities.

These clear qualitative examples of free energy, enthalpy and entropy changes make it easier to move forward into quantitative studies.

If you don't intend to go further with the experiments explained below, the low cost HTT1 shown in Figure 1 will be adequate. The tanks are made of steel and must not be submerged in water. If you intend to follow the instructions below, you need the HTT2 with stainless steel tanks.

Clausius-Clapeyron Equation

The formation and decomposition of metal hydrides is comparable to condensation and vaporization of liquids. Advanced students may wish to look deeper into the changes that occur in the solid phase as hydrogen (H1) comes and goes. The activity of H1 in the solid state is expressed as P 0.5 .

The pressure of hydrogen gas in equilibrium with a metal hydride increases rapidly with temperature. If we put a metal hydride reaction vessel into a variable temperature water bath (don't do this with the HTT1), we can record equilibrium pressures at various temperatures. For example:

We can now convert the data into units that are useful for applying the Clausius-Clapeyron equation--inverse temperature (1/Kelvins) and the natural log (base e) of pressure:

If we plot the converted data we get a straight line, as shown below in Figure 2. This is known as the "van't Hoff plot".

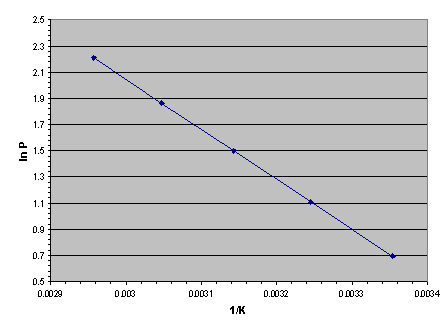
Figure 2. The "van't Hoff plot" of any substance that has a measurable vapor or sublimation pressure is a straight line in coordinates of absolute pressure logarithm versus inverse absolute temperature. This includes water, dry ice, liquid ammonia and metal hydrides.

The slope of a van't Hoff plot is linearly related to the latent heat (ΔH) of a vaporizing or subliming substance. The Clausius-Clapeyron equation is:

I. dP/P = ΔH dT/RT²

Where R is the universal gas constant, 8.314 Joules per gram-mole of ideal gas per Kelvin.

Integration of Equation I between two points on the van't Hoff plot yields:

ln (P₂ /P₁ ) = ln P₂ - ln P₁ = -ΔH/R (1/T₂ – 1/T₁ )

Solving for ΔH gives:

II. ΔH = -R (lnP₂ – lnP₁ )/ (1/T₂ – 1/T₁ )

From the set of converted data above, let's use the highest pressure and temperature as P₂ and T₂ and the lowest pressure and temperature as P₁ and T₁ . Substituting these values into equation II gives the latent heat of desorption:

ΔH des = +31773 Joules per gram-mole of H₂ .

The plus sign tells us that this much heat must enter the reaction vessel per gram-mole of H₂ desorbed. The best of metal hydrides are nearly reversible so, for absorption, we may write:

ΔH abs = -31773 Joules per gram-mole H₂ .

The sign of the enthalpy change is negative because heat flows out of a reaction vessel during absorption of hydrogen.

Standard Conditions

"Standard" conditions are needed to solve Gibbs' function from a set of experimental pressure-temperature data. The usual standard environment is 25℃ (298.15K) and 1 atmosphere (760 millimeters of mercury or 101.3 kPa). The conventional notation for standard Enthalpy is ΔH^o.

We just derived ΔH over a range of temperature-not at exactly 298.15K. If we wanted to know ΔH^o very precisely we would need high precision pressure-temperature data in a narrow range around 298.15K. This is true because ΔH is the difference between the enthalpies of the final and initial substances involved in the change. In the case of desorption, the final substances are metal and hydrogen. The initial substance is metal hydride. When we warm or cool a substance its enthalpy changes according to:

ΔH = m_pΔT

where m is the mass of substance in grams, c p is the specific heat in Joules per gram per Kelvin at constant pressure and ΔT is the temperature difference in Kelvins. This type of enthalpy change is called "sensible heat".

We can ignore sensible heat effects only if we know that the cps of all substances do not change significantly over the range of temperature of our data (298.15K to 338.15K). The specific heat of hydrogen increases from 14.31 to 14.54 over our temperature range-a change of +1.7%. Typical metals vary by twice as much. We do not have c p versus T data for most modern hydride alloys or their hydrides. We cannot believe a 5 significant digit result like ΔH^o des = 31773 Joules per gram-mole of H₂ . A detailed error analysis would probably justify a result like:

ΔH^odes = 32±1 kJoules per gram-mole of H₂ .

Standard Gibbs Free Energy Change

The standard Gibbs free energy change is the maximum reversible work that can be obtained from a mole of ideal gas at standard temperature against the resistance of standard atmospheric pressure. Hydrogen is very nearly ideal at moderate pressures and temperatures. Any thermodynamics text will derive

ΔG^o = RT^o ln(P/P^o)

as the standard Gibbs free energy change per mole of ideal gas produced. The metal hydride we tested produces 2.00 atmospheres of hydrogen pressure at 298.15K. Therefore, we calculate as follows:

ΔG^odes = 8.314 Joules/g-mol H₂^.K x 298.15K x ln(2/1)

= 1718±13 Joules/g-mol H₂ .

The accuracy of this result depends on the accuracy of the pressure and temperature instruments and the ideality of hydrogen gas. If the data are within ±0.1K and ±0.01 atm, we know ΔG^odes within ± 13 Joules/g-mol H₂ . ΔG^odes is positive because the 2.00 atmosphere H₂ produced has the ability to do work on the 1 atmosphere standard environment.

Standard Entropy

We may now calculate the standard entropy of desorption because it is the only unknown remaining. By rearrangement of Gibbs' function:

ΔS^odes = (ΔH des^o - ΔG des^o)/T^o,

ΔS^odes = [(32 - 1.7) kJoules/g-mol H₂ ] / 298.15K = 102±4 Joules/g-mol H₂^.K.

ΔS^odes is positive because a cloud of desorbed gas is more disordered than hydrogen within a solid metal hydride crystal. There was also a small negative change in the entropy of the solid. The net entropy change calculated above is the algebraic sum of the two entropy changes.

Gibbs' Phase Rule

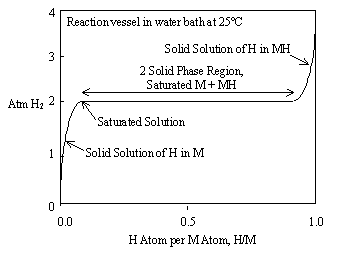
Figure 3. Pressure vs. composition isotherm for an ideal metal hydride

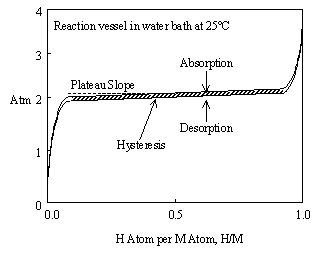
Figure 4. Real metal hydrides usually have slope on their plateaux and a pressure difference between the absorption and desorption plateaux. This difference is called "hysteresis".

The expression of hydrogen content as H/M is a convention that simplifies more complex expressions, like LaNi 5 H 6 . Since there are 6 hydrogen atoms and 6 metal atoms we can say, H/M = 1 to describe the saturated hydride phase.

At the midpoint of the plateau in Figure 3, H/M = 0.5. At this point we have 50% hydrogen-saturated metal and 50% metal hydride in equilibrium with hydrogen gas. We are now ready to examine this situation in the light of Gibbs' Phase Rule and to understand why there must be a pressure plateau in a metal hydride isotherm. First some definitions:

A "phase" (φ) is a portion of matter that is homogeneous and physically distinguishable from surrounding matter. Familiar examples of phases are gases, liquids and solids. Air is a mixture containing several gases but just 1 phase. Alcohol in water is just 1 phase. Salt and pepper, no matter how well mixed, are two distinct phases.

A "component" (C) in Gibbs' Phase Rule has a unique chemical identity. Alcohol in water is a single phase with 2 components. Hydrogen, in the gaseous phase, dissolved in metal, or part of a metal hydride crystal, is a single component. A hydrideable metal like Mg is clearly 1 component. A hydrideable intermetallic compound, like LaNi 4 Al, contains 3 elements that act together as 1 component, M.

A "degree of freedom" (F) is an independent intensive variable, like pressure, temperature or voltage, used to describe the state of a system. Intensive variables are contrasted with extensive variables, like volume or mass.

Gibbs' Phase Rule is:

φ + F = C + 2

At the midpoint of the hydride plateau (H/M = 0.5) in Figure 3, we have hydrogen in the gaseous phase and two distinct solid phases-hydrogen saturated metal and metal hydride.

The boundaries between the two solid phases can be seen with a microscope. At the left edge of the plateau, crystals of hydride begin to form (nucleate) at distinct locations on the surfaces and in grain boundaries of the metal crystals. The hydride crystals grow, consuming saturated metal and hydrogen gas, as we move from left to right across the plateau. At the right side of the plateau there is no more saturated metal phase. It has all been converted to hydride phase.

If we apply Gibbs' Phase Rule at any place between the end points of the plateau, we find 3 phases; saturated metal, metal hydride and hydrogen gas, so φ = 3. There are 2 components, H and M, so C = 2. Therefore F must be 1 to balance the Phase Rule. We have just 1 degree of freedom. Such a system is said to be "univariant". We can try to increase the pressure by adding a small amount of hydrogen, but the temperature is held constant by the surrounding water bath. Pressure and temperature have a fixed relationship in a univariant system. We defined that relationship when we measured the van't Hoff plot, Figure 2. The pressure will fall as hydrogen is consumed in the formation of additional metal hydride phase until equilibrium is restored. Heat (-ΔH abs ) is removed from the reaction vessel by the water bath.

The converse is also true. Removing a small amount of hydrogen at constant temperature does not change the pressure. Heat (+ΔH des ) enters the reaction vessel from the surrounding water bath and desorbs hydrogen until the equilibrium pressure is restored.

If we remove the reaction vessel from the water bath and wrap it with insulation, we can warm it up by adding hydrogen. ΔH abs cannot escape very quickly through good insulation so it warms the materials inside. These materials include the saturated metal, the metal hydride, the hydrogen gas and the reaction vessel itself. Let's say there are k different materials and that we know the mass and specific heat of each. The temperature inside the insulation will rise until:

where n is the number of moles of hydrogen absorbed. The new pressure and temperature will fall on the line in Figure 2.

To the left of the plateau in Figure 3 we have a solid solution of hydrogen in metal. Regardless of how much hydrogen is dissolved in it, there are only metal crystals and hydrogen gas--no hydride crystals. We have just 2 phases, so φ= 2. The components remain hydrogen and metal, so C = 2. Gibbs' Phase Rule then gives us 2 degrees of freedom. We can apply any hydrogen pressure from zero to just below the plateau pressure. Small amounts of hydrogen will be absorbed and desorbed from the solid solution but there are no phase changes. We can cool or warm the reaction vessel and maintain any pressure we choose by adding or releasing small amounts of hydrogen. There is no fixed relationship between pressure and temperature in a solid solution region. Circumstances with 2 degrees of freedom are known as "bivariant".

The same can be said about the solid solution of hydrogen in the metal hydride phase to the right of the plateau. There is the hydrogen gas phase and one solid phase-metal hydride. This region is also bivariant.

Procedures

We can use the simple apparatus shown in Figure 1 to do the following:

• Give students tactile, visual and intuitive examples of the terms in Gibbs' function
• Make it clear that the terms are signed quantities
• Collect experimental data and draw a van't Hoff plot
• Calculate standard enthalpy change from the slope of the van't Hoff plot
• Calculate standard Gibbs' free energy change from the mid-plateau hydrogen pressure at 25℃
• Calculate standard entropy change using Gibbs' function and the preceding results
• Learn to apply Gibbs' Phase Rule under univariant and bivariant conditions

Apparatus and Instructions

You may opt to buy the device shown in Figure 1 only, and plan your own experiments.
Fuelcellstore.com also offers step-by-step instructions for conducting each of the experiments discussed above.

A silicone fabric electric heater is wrapped around Tank A to recharge the device prior to each use. This is the only authorized way to heat the device. NEVER APPLY A FLAME!

Instruction Sets 2 through 4 are meant to be 1-hour classes for university-level students of chemistry, thermodynamics or materials science. Students should have a copy of the above document before carrying out the Instruction Sets. A limited license to duplicate the above document for use within your educational institution is packaged with the device. Questions for exams are included with each Instruction Set.

Products

Model HTT1 Demonstration Device (steel tanks, don't submerge in water): $699

Model HTT2 Demonstration Device (stainless tanks may be submerged in water): $799

Replacement Electric Heater (a heater is packaged with each new HTT): $82

Instruction Set 1
Basic unpacking, setup, recharging and safety instructions (free with HTT1 or HTT2)

Instruction Set 2
A visual and tactile demonstration of enthalpy and free energy changes as signed terms in Gibbs' function plus a graphical explanation of entropy changes in absorption/desorption processes: $114

Instruction Set 3
Procedures for taking data, making a van't Hoff plot and using the data to calculate standard enthalpy, free energy and entropy changes: $114

Instruction Set 4
Procedures for demonstrating Gibbs' phase rule in univariant and bivariant conditions: $114